Last year, we began reviewing curriculum resources for middle school math.  When we put out the proposal asking for submissions, we asked for some very specific things based on recommendations from the National Council of Teachers of Mathematics (NCTM).

Some of the recommendations and research we used in identifying high quality instructional materials are listed below.

We used 8 Effective Teaching Practices from NCTM’s publication Principles to Actions.

1. Establish mathematics goals to focus learning. 
2. Implement tasks that promote reasoning and problem solving.
3. Use and connect mathematical representations.
4. Facilitate meaningful mathematical discourse.
5. Pose purposeful questions.
6. Build procedural fluency from conceptual understanding.
7. Support productive struggle in learning mathematics.
8. Elicit and use evidence of student thinking.

According to Hattie’s research, Teacher Estimates of Achievement had an effect size of 1.62 and Collective Teacher Efficacy had an effect size of 1.57.

We utilized the research presented by Jo Boaler on the brain’s ability to grow and change to set the stage for holding high expectations for all students.  We knew that quality tasks for students was a must have.  Rigorous tasks with multiple entry points.

However, we were also looking for resources that would build teacher capacity.  We weren’t looking for another resource that would have teachers reading out of a textbook.  We wanted to shift instruction and pedagogy in a way that would develop students as critical thinkers and problem solvers and teachers as facilitators of learning, not keepers of information.

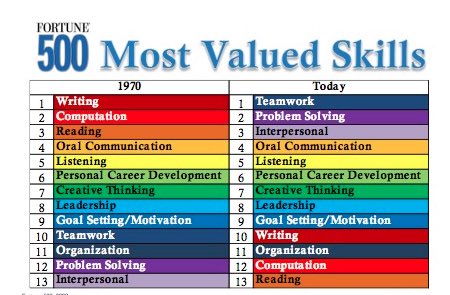
This graphic has showed up in many places, but I first saw a similar one in Boaler’s book, Mathematical Mindsets.

On first look, it made me think of the book, Hidden Figures.  The women in the retelling were hired by NASA to be computers.  Their job was to crunch numbers, and to do it fast.  However, with the arrival of the computer, the women were faced with becoming obsolete to a machine.  So they adapted by becoming what NASA needed most at that time, problem solvers.

It was clear that if continue to teach math in the way we always have, we will produce the same types of thinkers; students who are able to follow directions and procedures; computers.  What the world’s largest companies are asking for are thinkers.  Students who have been taught how to think about problems in new ways and approach them from multiple pathways.  Students who can work collaboratively to come to a solution.

This is what we knew we needed – instructional materials that were student-centered;  Resources that allowed kids to make sense of problems and persevere in solving them.

Which leads me to another set of standards that played a huge part in selecting a resource; The Standards for Mathematical Practice.

The content standards get a lot of attention across the country, but many people (even some math teachers) are unaware that there are also a set of standards for mathematical practice.

These are the employable skills that are essential for our students to leave our systems with.  Many of us have heard the quote mentioned by Richard Riley, former US Secretary of Education, 

“We are currently preparing students for jobs that don’t yet exist, using technologies that haven’t been invented, in order to solve problems we don’t even know are problems yet.”

So the question remains, how DO we prepare students for such a world?  If we use employable skills as a model, all signs point to developing students who can think, reason, and solve problems as part of a team.

In our search, we reviewed several resources, one of which was Illustrative Mathematics.  Illustrative Mathematics was the highest ranked curriculum by http://www.EdReports.org, an independent non-profit designed to support schools and educators in evaluating instructional materials.

We took a team of teachers to a 4-day training in Atlanta, GA to evaluate it further.  The teachers were hooked and requested to pilot it the following year.  We opened the pilot up to all of our middle school teachers and many participated.

After piloting the resource, we collected feedback from teachers and heard things like, “Illustrative Mathematics has made me a better (more effective) teacher.”

“My students are talking about math in ways I never imagined they could.”

“One of my students who had never spoke in class before, came up and explained their strategy for a number talk today.”

They reported increases in demonstration of understanding on summative assessments, district benchmarks, and time spent on productive struggle.

The pilot experience was not easy.  Teachers struggled with the change in pedagogy.  They struggled with beliefs and practices that they had held and used for years being turned on their end.  They worried that students wouldn’t formalize concepts by the time standardized testing came along.  However, at the end of the pilot, teachers overwhelmingly wished to continue using the resource due to the growth they had seen in students thinking and reasoning skills.

We knew that in order to shift instruction in this way, we needed to support teachers with upfront and job-embedded professional learning opportunities.  So we arranged for Illustrative Mathematics trainers to come in to do a 2-day training for each of our teachers, SPED teachers supporting math, ELL coaches, Learning Specialists, Title 1 Support and any administrators who wished to attend.

We then planned four quarterly half day collaboration days for teachers at each grade band.  Tomorrow is our first collaborative day together and I am excited to continue our journey on refining our practice.

I’d love to hear stories from other districts and ideas of how to best support teachers in the continued implementation of problem-based instructional materials.

After falling in love with teaching mathematics in the classroom, I knew that I wanted to eventually end up in a learning support role for mathematics instruction.   Shortly after attending a Math Add+Vantage training offered by our district Title 1 department, I accepted a position as a K-5 Numeracy Coach.  I was trained shortly after as a Math Recovery Intervention Specialist.

I spent six years working with teachers on intervention and instruction.  The schools I worked in had some of the highest (over 85%) free and reduced lunch rates in our district.  Students came to us with varied educational backgrounds, many with very few experiences in numeracy.   In Title 1 Math, we utilized an instructional configuration for Math Workshop that the team had created based on the Comprehensive Literacy Model.  I worked with teachers to get math workshop and guided math set up in their rooms for those six years.  We looked at data, we visited other classrooms, we pre-assessed and re-assessed.  Our students were showing growth, but they weren’t making huge gains in proficiency.  The question was, why?

I learned many lessons in my years as a coach, but probably the one that has influenced my philosophy on education the most is that it is possible to intervene too much; and we were doing it.  I had set my expectations for students too low and was not exposing them to tasks that allowed them enough time and space for productive struggle.  We were so concerned with meeting students “where they are” that we had completely shifted instruction to intervention and removed the rigor.  I’d like to say that this realization came overnight, but the truth is it came after years of reading, learning, teaching, reflecting, and examining my practice.  To be honest, I’m still on the journey.

Two years ago, I accepted the curriculum coordinator position in our district for K-12 Mathematics.  The position had been re-imagined and was posted as Coordinator of 21st Century Numeracy.  When I accepted my current position, I was charged immediately with putting in place a math workshop model for all of our elementary buildings.  I was excited about this because I knew it would help teachers be more purposeful about instruction and this created opportunities to open dialogue about student understandings and next steps for instruction.

I told myself that we were doing workshop right because we had flexible groups that changed regularly.  But the truth was, in practice, that wasn’t the case in every classroom and even with flexible grouping, we were still tracking students into ability groups that stayed fairly stagnant.  Even though our practices were perhaps the best case scenario for math workshop, we were missing the boat on many other aspects of high quality instruction.

I also struggled with where and when to use high quality tasks such as 3 Act math tasks.  Our current structure did not allow for those opportunities.

It was really a perfect storm that led me to my current understandings and beliefs.

Jo Boaler‘s book, Mathematical Mindsets, spoke to my heart.  The findings that she proposed based on brain research that a) everyone can learn math at high levels, b) mistakes are really important in the learning process, and c) we must value depth over speed, made me look at our practices through a new lens.

It was Dan Meyer‘s Ted Talk that introduced me to 3 Act Math years and years ago that helped me develop my belief in problem based learning (and become obsessed with creating 3 Act math tasks for elementary).  I’ve had the opportunity to attend a few of Dan’s sessions at conferences since then and his words stuck with me, “Be Less Helpful.” 

I couldn’t reconcile those words against some of our instructional practices.  Everything we had designed to support students was about being more helpful – which had the effect of making them helpless.  We noticed that when students faced something difficult, they would immediately ask for help instead of persevering.  (For my thoughts on praise and learned helplessness, check out my prior blog post, How Do I Change Math Class Tomorrow?)

It was Robert Kaplinsky‘s Open Middle problems that provided the perfect model of how a task with multiple entry points could allow all students to engage in high quality math tasks.

It was Christopher Danielson‘s books, Which One Doesn’t Belong and How Many?, that tugged at the importance of sense making.

It was Sherry Parrish‘s book, Number Talks, that allowed me to look at fact fluency and number sense in a whole new light.

It was Brian Bushart‘s Numberless Word Problems, Steve Wyborney‘s Estimation Clipboard, Fawn Nguyen‘s Visual Patterns…the list goes on and on.

It was Graham Fletcher‘s link between 3 Act Math and the 5 Practices that had me looking at the power of combining high quality tasks and intentional teacher moves.

In 2017, at the NCSM National Convention, I was given a copy of Jennifer Lempp‘s new book, Math Workshop.  In her book, Jennifer proposed a mix of guided math days and what she calls task and share days.  Task and share days were essentially days in which students work in heterogeneous groups to solve problems and share their solutions with the class. 

It was after reading her book that I realized it was time to modify our instructional model.  The following year we introduced two instructional models: Math Workshop days and Problem Solving days.  

That was our first step in a journey toward equitable teaching practices.

I truly believe that the lack of quality tasks (with multiple entry points) is the reason we have struggled with mathematics instruction for so long and why we have not been able to shift our pedagogy from teacher-centered to student-centered instruction.  As the list above clearly shows, that time is over.  In my future blog posts, I will share other open source resources for high quality curriculum that puts students in the drivers seat of enduring understanding.