I tried out the Gatorade is Thirst Aid task with five classrooms this past week. Three 4th grades (2 were combined) and two 5th grades.
I knew there would be misconceptions about measurement, but the information we gained was invaluable in really pinpointing where students were struggling with conversion. It was pretty interesting to see that it differed at each grade-level. Probably because they both just finished units on Measurement and were learning slightly different standards.
Interestingly enough, our 4th grade students had a better grip on how many ounces per cup and the fact that we needed to multiply or divide to find the answer. They also had a better grip on how to use the remainder. Many started by writing in cups and ounces and then when asked if there was another way to write it, came up with the mixed number of cups.




Our 5th grade students had the misconception that there were 16 ounces in a cup. They were no doubt thinking ounces in a pound, but it was interesting that many of the students had this same thought. What I have noticed with this group of students is that they often try to over-complicate the process when solving 3 act tasks. They think there is a trick in there somewhere which leads me to believe that they don’t have a firm conceptual basis of how to work with numbers and operations.
I noticed two misconceptions that really stood out to me. One student wrote his answer as 3.4 cups because there were 3 cups with 4 ounces remaining. He did not see the remainder as a part of the composite unit 8, but instead wrote it as four tenths in decimal form. Does this student have a firm understanding of decimal place value?
The other misconception that I thought was really interesting was that the solution could be written as 3/5 cups in fraction from because the decimal notation was 3.5. This one really got me thinking about how to integrate fractions and decimals more thoroughly as related concepts.
And the part that I love: “What’s the Math?”


Gumball Activity
Today, with those two 5th grade classes, we did the gumball activity I mentioned in a previous post and it was really surprising to see that many of the students did not have firm grip on 36″ in a yard” or “100 cm in a meter.” They struggled less with visualizing a square meter than the last class, but instead had a difficult time determining how many inches were in a yard, and how to tell how long a meter was. I did a lot of questioning with these groups like, “how many inches are in a foot? How many feet in a yard?” and “what do you know about metric measurements? Why are they easier to work with? How could you use that to help you?” A few students were able to tell me that they are in tens, but many then decided that 10 cm was a meter. I showed them the size of 10 cm and asked, “does that make sense?” They agreed it didn’t and then were able to tell me it would be 100. They were pleasantly surprised when they saw that the measurement tape they were using was exactly 100 cm long!
One of the most surprising things I noticed was that many students could not agree on an approach to the question, “how many gumballs across is the sidewalk?” I saw measuring tapes laid across the sidewalk, I saw gumball lining the edges and I had students asking me how to solve this one. I assumed (yes I know) that measuring with non-standard units would be the easy one for them, but they were trying to find some way to measure the gumballs and count and couldn’t come up with a solution. When I asked them to reread the question, I asked, “where would you start?” They were able to say, “counting the gumballs.” I then asked, “do you need a measurement tool for that?” That’s when it hit home.
We asked students several clarifying questions after we completed the activity. When we asked students how many centimeters in a meter, they were able to tell us. When I asked “how do you know?” A student said, “because I saw it on the stick when I was measuring.”
This just firmed up the hypothesis we had that measurement is best taught in context. The teachers and I discussed how we might change our measurement lessons next year to allow them to have more experiences measuring and converting with objects.
I asked a student, “why do you think we did this activity today?” I was saddened when the reply was, “because it might be on the MAP test.”
I knew it was time to interject and bring in some examples of when and where they might see this in their daily lives. I said, “yep, it might be on the MAP test, but let me tell you why I care about what we did today. I am getting ready to re-seed my lawn and seed bags come by how many square yards the bag of seed will cover. If I didn’t know how big a square yard was or wasn’t able to calculate about how many square yards in my lawn, I might buy too much seed or not enough. Those bags are heavy and I only want to buy what I need. Here is another example: I recently repainted my son’s room. Paint comes in gallons that tell me how many square feet the paint will cover. Does anyone know how I would figure that out?”
Student: “that’s area.”
Me: “You’re right, and how would I find the area of the wall?”
Another Student: “length times width.”
Me: “Yep, so how would I find the area of the wall?”
Another student: “The same way. Measure the length and width of the wall.”
Me: “And then what?”
Student: “multiply it.”
And yes, I did tell them that I don’t want them to know this because it’s gonna be on the MAP test, I want them to know because it will be important to them when they own their own home.
What I gained from this activity is the fact that when planning projects such as this, it is so very important to include many types of question sets that span the grade-levels especially those leading up to the current. Many times, we as teachers assume that students have a firm grip on a concept because it was taught many grades before, but we really have no way to gauge their experiences before they enter our classroom.
Assume nothing.












 Each of my teachers share their Canvas page with me, so I created a page that would be very easy to navigate for students and embedded the
Each of my teachers share their Canvas page with me, so I created a page that would be very easy to navigate for students and embedded the 





















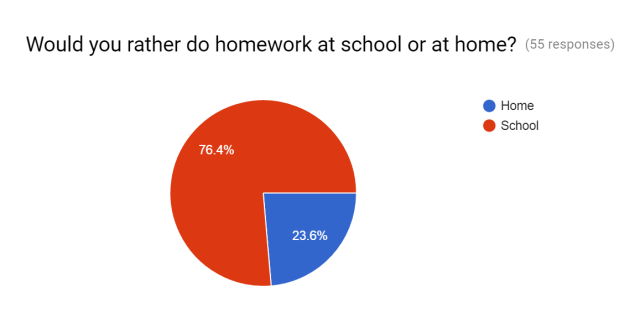
 We decided to open up the school in the morning to them, do a week of project based homework and a week of flipped lessons and give the survey again. We also decided to start with 4th grade math and bring in 5th grade when we could gauge the number of students we would have in attendance. We are sending home a letter to parents explaining the change and will start next week!
We decided to open up the school in the morning to them, do a week of project based homework and a week of flipped lessons and give the survey again. We also decided to start with 4th grade math and bring in 5th grade when we could gauge the number of students we would have in attendance. We are sending home a letter to parents explaining the change and will start next week! students immediately started solving the problem and raising their hands to tell me the solution. I reiterated the fact that I was not looking for a solution, I simply wanted them to think about how we would represent 1 or one whole in fraction form.
students immediately started solving the problem and raising their hands to tell me the solution. I reiterated the fact that I was not looking for a solution, I simply wanted them to think about how we would represent 1 or one whole in fraction form.








